Search Search

Parametric modelling of survival following HIV and AIDS in the era of highly active antiretroviral therapy: data from Australia

PDF version

Research article

F. Nakhaee 1,2 and M. Law1

مُتُثَابتات البُقيا على قيد الحياة بعد الإصابة بالإيدز أو العدوى بفيروسه في حقبة المعالجة الشديدة الفعالية بمضادات الفيروسات: معطيات من أستراليا

فاطمة نخعي - ماتيولا

الخلاصـة: إن نماذج مُتُثَابتات البُـقيا لم تُطبَّق من قبل للتنبُّؤ بالبُقيا على قيد الحياة بعد تشخيص مرض الإيدز أو العدوَى بفَيْروسه في أستـراليا. وقد طُبقت أربعة نماذج مختلفة من المتثابتات وهي النموذج الأُسِّي، ونموذج ويبول Weibull، ونموذج اللوغارتم الطبيعي، ونموذج اللوغارتم اللوجستي- على معطيات الحالات الإيجابية للعدوى بفيروس الإيدز والحالات المُشَخَّص إصابتها بالإيدز والتي حُصِلَ عليها عن طريق نظام التـرصد الوطني للإيدز والعدوى بفيروسه. وباستخدام الأرجحية المستندة على معيار جودة التواؤم وجد أن نموذج ويبول Weibull كان أفضل نماذج التواؤم للتنبؤ بالبُقيا على قيد الحياة بعد تشخيص العدوى بفيروس الإيدز مع أو بدون تشخيص الإصابة بمرض الإيدز. وقد جرى دمج العديد من المتغيّرات المشاركة – كالعمر، والجنس، وفئة التعرّض المشترك لفيروس الإيدز، وعدد الخلايا CD4، والمعالجة بمضادات الفيروسات، والعلل المعرِّفة بالإيدز- في الطراز المتثابت للتنبؤ بالعوامل المتـرابطة مع الوفيات المستقبلية. وقد توافقت الوفيات التي جرى التنبؤ بها مع الوفيات التي شوهدت عقب العدوى بفيروس الإيدز أو الإصابة بمرض الإيدز. مما يبرِّر تطبيق نموذج ويبول في الإسقاطات المستقبلية على الوفيات الناجمة عن الإيدز والعدوى بفيروسه.

ABSTRACT: Parametric survival models have not previously been applied to survival following a diagnosis of HIV/AIDS in Australia. Four different parametric models—exponential, Weibull, log-normal and log-logistic—were applied to data both on HIV-positive cases and on cases diagnosed with AIDS collected through the national HIV/AIDS surveillance system. Using likelihood based goodness-of-fit criteria the Weibull model was found to be the best-fitted model for predicting survival following a diagnosis of HIV infection without and with a diagnosis of AIDS. Several covariates—age, sex, combined HIV exposure category, CD4 cell counts, antiretroviral treatment and AIDS-defining illnesses—were included in the parametric model to predict factors associated with future mortality. Predicted deaths were in agreement with the observed deaths following HIV infection and AIDS. The Weibull model will be applied for future projections of deaths from HIV/AIDS.

Modélisation paramétrique de la survie après un diagnostic d’infection à VIH ou de sida à l’ère du traitement antirétroviral hautement actif : données d’Australie

RÉSUMÉ: Les modèles paramétriques de survie n’ont pas été utilisés précédemment pour évaluer la survie après un diagnostic d’infection à VIH/sida en Australie. Quatre modèles paramétriques différents — le modèle exponentiel, la loi de Weibull, le modèle log-normal et le modèle log-logistique — ont été utilisés sur les cas positifs au VIH et sur les diagnostics de sida recueillis dans le cadre du système de surveillance du VIH/sida pour le pays. À l’aide des critères de validité de l’ajustement reposant sur la probabilité, le modèle de Weibull s’est avéré être le modèle le mieux ajusté pour prédire la survie après un diagnostic d’infection par le VIH avec ou sans diagnostic de sida. Plusieurs covariables — l’âge, le sexe, la catégorie d’exposition au VIH associée, la numération des lymphocytes T‑CD4, le traitement antirétroviral et les pathologies classantes pour le sida — ont été incluses dans le modèle paramétrique pour la prévision des facteurs associés à une mortalité prévisionnelle. Les prévisions de mortalité correspondaient aux décès observés après un diagnostic d’infection à VIH ou de sida. Le modèle de Weibull sera utilisé pour les projections de mortalité liée au VIH/sida.

1Department of Biostatistics and Epidemiology, Faculty of Health, Kerman University of Medical Sciences, Kerman, Islamic Republic of Iran (Correspondence to F. Nakhaee: This email address is being protected from spambots. You need JavaScript enabled to view it.).
2National Centre in HIV Epidemiology and Clinical Research, Faculty of Medicine, University of New South Wales, Darlinghurst, New South Wales, Australia. Received: 28/06/09; accepted: 30/08/09

EMHJ, 2011, 17(3): 231-237

 Introduction

 

Survival analysis methods that measure the risk of death or progression of a disease provide predictions that help clinicians to estimate trends in their patient outcomes. Those methods also allow health planners to predict the HIV burden on the health system and to allocate health service resources appropriately.

The natural history of HIV disease—the time from HIV seroconversion to AIDS diagnosis (incubation period) or to death (survival time)—has been modelled using a number of parametric and non-parametric survival models, especially since the introduction of highly active antiretroviral therapy (HAART) in 1996 [1–7]. Survival times vary according to a number of factors, including sociodemographic factors, CD4 cell counts, HIV viral load and AIDS-defining illnesses. These covariates are entered in the models allowing predictions of their effects on the time to development of AIDS and to death. Cox regression, a semi-parametric model, has been widely used for this, because fewer assumptions are needed to predict the prognostic factors associated with survival. Parametric models, however, are known to be more accurate than non-parametric methods when using survival models to make projections about the risk of death [8,9] and future trends in mortality [10]. Concurrent with developing survival models based on HIV and AIDS data, investigators have attempted to assess the goodness-of-fit and validity of parametric models [2,3,11–13].

The study reported here was the first in which parametric models were applied to data both on HIV-positive cases and on cases diagnosed with AIDS collected through the national HIV/AIDS surveillance system in Australia. Goodness-of-fit criteria were used to find the best model for predicting survival following a diagnosis of HIV infection without and with a diagnosis of AIDS.

 Methods

Four parametric models—exponential, Weibull, log-normal and log-logistic—were used. All models were fitted to 2 datasets. The HIV dataset included individuals who were diagnosed as HIV positive but without a diagnosis of AIDS or who subsequently developed AIDS but before the AIDS diagnosis was reported to the National HIV Registry. The AIDS dataset consisted of individuals diagnosed as HIV-positive and also diagnosed with AIDS who were registered in the National AIDS Registry. Both HIV and AIDS cases diagnosed from 1980 to the end of 2003 were linked with the national death index [14], then HIV infection and AIDS diagnoses between 1997 and 2003 were used separately to model survival following acquisition of HIV infection and development of AIDS. Survival time was calculated from the date of the diagnosis of HIV infection or of AIDS to the date of death or, if alive, at 31 December 2003. HIV-positive cases who were subsequently diagnosed with AIDS were censored at the date of the AIDS diagnosis in the HIV dataset.

The approvals of the ethics committee at the University of New South Wales and Australian Institute of Health and Welfare were obtained to perform the linkage between HIV and AIDS diagnoses with the national death index data.

Several covariates—including age, sex, combined HIV exposure category, CD4 cell counts, antiretroviral treatment and AIDS-defining illnesses [such as Pneumocystis jiroveci, other infections, Kaposi sarcoma, non-Hodgkin lymphoma, wasting syndrome, central nervous system (CNS) conditions]—were included in the parametric model. Since individual data on antiretroviral treatment were not available, 2 covariates were created: one representative of the percentage of patients treated with mono- or double therapy estimated from the literature [15–17] and the other representative of patients treated with HAART. The percentage of patients receiving HAART prior to an AIDS diagnosis were extracted from data collected for the Australian government’s S100 highly specialized drug programme and the percentage of patients receiving HAART after AIDS diagnosis were estimated from the Australian HIV observational database [18]. These 2 covariates were included in the parametric model as time-dependent variables, with all patients alive in a given calendar year having a covariate value for treatment corresponding to the proportion of all patients receiving treatment in that year. The reason for adopting the percentage on mono- or double therapy or HAART as covariates in the parametric models was to allow projections of mortality to be made under different scenarios of future treatment. Age was included as a time-dependent variable in the models to adjust for the effect of age on treatment.

The maximum likelihood method and the Akaike information criterion (AIC) [3,12,13] were used to assess the best parametric model fitted to both the HIV and AIDS datasets.

One approach to assess the model fit would be to compare the number of deaths which were observed following HIV infection both without/before AIDS and after AIDS diagnosis with the number of deaths predicted by the parametric model [5]. When predicting mortality using the parametric models, it is necessary to extend follow-up for subjects who died to avoid predictions underestimating the number of deaths. Thus the predictions are based on the numbers of deaths estimated by the models if all subjects had completed follow-up. The 2 datasets included the same covariates but the follow-up period was extended for subjects who had died to the end of the study at 31 December 2003. The parametric model estimated from the original datasets was then applied to these datasets with extended follow-up to obtain the predicted probability of death according to each subject’s covariate pattern. The expected number of deaths predicted by the models was then simply the sum of the predicted probabilities of death across all subjects. The expected numbers of deaths estimated from the fitted model were compared with the observed deaths following both HIV and AIDS diagnoses in total, by calendar year, and in terms of fixed effect covariates to assess the fit of the model.

Results

Best fitting model

Table 1 shows the log likelihood and AIC statistics for the 4 parametric models applied to the survival data in order to select the best fitting parametric model. According to these criteria, the Weibull model achieved the lowest AIC value and was therefore the best model for predicting survival of HIV-positive cases both without/before a diagnosis of AIDS and with a diagnosis of AIDS.

Table 1 Selection of the best-fitted model for the HIV dataset (cases diagnosed as HIV-positive without AIDS diagnosed or before a diagnosis of AIDS) and the AIDS dataset (cases diagnosed as HIV-positive after a diagnosis of AIDS), applying 4 different parametric models

Survival of cases diagnosed as HIV-positive without/before AIDS

The hazard ratios of survival of HIV-positive cases without/before a diagnosis of AIDS, estimated from the Weibull model, are shown in Table 2. The following factors were significantly associated with increased risk of death in HIV-positive cases: age 40+ years (compared with ages 30–34 years as the reference category) (P < 0.001); male injection drug user (IDU); haemophiliac patient; and male with other exposures, including cases of mother-to-child HIV transmission among children and adults/adolescents without a reported sexual or blood exposure (compared with homosexual men) (P < 0.01). Being on antiretroviral treatment was not statistically significantly associated with increased risk of death following diagnosis of HIV infection without/before AIDS and therefore survival was improved.

Table 2 Covariates of survival of cases diagnosed as HIV-positive without/before a diagnosis of AIDS, applying the Weibull model, 1997–2003

Observed and predicted deaths among people diagnosed with HIV without AIDS are shown in Figure 1 by calendar year between 1997 and 2003. The predicted deaths were closely in agreement with the observed deaths. In addition, a test was performed to compare the goodness-of-fit of the observed deaths of the HIV-positive cases without/before AIDS with the predicted deaths by the Weibull model. For deaths during this period, the goodness-of-fit was χ2 = 0.588 (P = 0.997), suggesting no evidence of a significant lack of fit. These results are in agreement with a visual comparison of the observed and predicted deaths in Figure 1.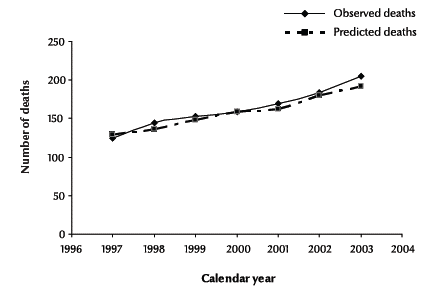

Figure 1 Observed and predicted deaths of cases diagnosed as HIV-positive without/before a diagnosis of AIDS by calendar year, 1997–2003
Figure 1 Observed and predicted deaths of cases diagnosed as HIV-positive without/before a diagnosis of AIDS by calendar year, 1997–2003

 Survival cases diagnosed as HIV-positive with AIDS

Table 3 shows the hazard ratios of survival of HIV-positive cases with a diagnosis of AIDS. A higher CD4 cell count at AIDS diagnosis was significantly associated with a lower risk of death after the diagnosis of AIDS. During this period of follow-up the following factors were found to be significantly associated with an increased risk of death: age group 25–29 years (P = 0.007); age 50+ years (P < 0.001); male IDU (P = 0.043); and having non-Hodgkin lymphoma, a CNS condition or one or more other illness (compared with Pneumocystis jiroveci as the reference) (P < 0.001). As expected, being on antiretroviral treatment was also associated with improved survival among AIDS patients.

Table 3 Covariates of survival of cases diagnosed as HIV-positive with a diagnosis of AIDS, applying the Weibull model, 1997–2003

Figure 2 demonstrates the observed and the predicted deaths following a diagnosis of AIDS by calendar year from 1997 to 2003. The comparison of observed deaths and predicted deaths showed that the model fitted reasonably. The goodness-of-fit of the model was χ2 = 11.86 (P = 0.065), suggesting no evidence of a significant lack of fit.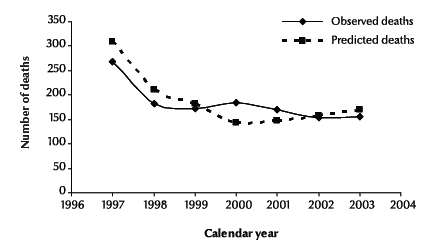

Figure 2 Observed and predicted deaths of cases diagnosed as HIV-positive with a diagnosis of AIDS by calendar year, 1997–2003
Figure 2 Observed and predicted deaths of cases diagnosed as HIV-positive with a diagnosis of AIDS by calendar year, 1997–2003

 

Discussion 

Survival following a diagnosis of HIV infection was modelled by applying parametric survival models on people who were only diagnosed with HIV or with HIV and AIDS registered in the national surveillance system from 1997 to 2003. Applying likelihood-based criteria for model selection indicated that the Weibull model was the best-fitting parametric model for predicting survival following both HIV and AIDS diagnoses.

Although the Cox model is frequently used in survival analysis, parametric models were selected to estimate the survival probabilities in this study because these models are known to be more accurate for projections, and also because the baseline hazards function is not estimated by the Cox model [11]. Furthermore, parametric models allow survival probabilities to be projected beyond the observed follow-up period [10]. Parametric models therefore permit deaths following a diagnosis of HIV infection and AIDS to be projected into the future.

The same approach of applying parametric survival models to obtain the best-fitted model for HIV disease progression to AIDS or to death has been used in some longitudinal studies [2,3,6,9,10,19]. Our finding that the Weibull model was the best-fitted model for both the HIV and AIDS datasets were in agreement with the models developed previously in other cohorts [2,11].

The Weibull model predicted an increased risk of death after the diagnosis of AIDS in the age group 25–29 years and also for cases diagnosed as HIV-positive without AIDS and after AIDS in the age group 50+ years. Our finding of shorter survival for older ages of HIV-positive cases both without AIDS and after AIDS diagnosis is consistent with other studies [19–21]. Poorer survival in older ages may reflect the difference in initiation of antiretroviral treatment among older persons, especially as Phillips et al. have demonstrated that the decline in CD4 cell counts is faster among older age groups [21]. It is also notable that the age at diagnosis of both HIV and AIDS has increased in Australia over the last decade. The median age of HIV infection diagnosis among men increased from 32 years prior to 1996 to 37 years in 2005, while the median age at AIDS diagnosis among men increased from 37 years to 42 years over the same period.

Our study found that men who were IDUs experienced reduced survival times for HIV without AIDS and after AIDS diagnosis compared with other exposure categories. The increased risk of death for both HIV-positive cases and those with AIDS among male IDUs in the post-HAART era may be due to non-adherence to treatment or because current and former IDUs are known to have an increased risk of death from non-HIV-related causes [22]. In another study a reason for poorer survival among IDUs was suggested to be limited access to treatment as only 45% of IDUs had initiated HAART 5 years after seroconversion compared with 57% of non-IDUs [7]. The percentage of IDUs diagnosed with AIDS has also increased in Australia from 4.8% in 1997 to 6.4% in 2003 [23].

In our study cases whose HIV infection was attributed to receipt of blood or treatment for haemophilia/coagulation disorders experienced poorer survival times following a diagnosis of HIV-positivity prior to AIDS diagnosis than other HIV exposure categories, possibly reflecting the effect of haemophiliac disease on mortality. This is consistent with a previous study on pre-AIDS mortality that found haemophiliac patients had poorer survival following HIV diagnosis prior to AIDS diagnosis compared with other HIV exposure categories [24].

To estimate the effect of treatment on the risk of death, covariates including the percentage of antiretroviral therapy were entered into the model. Survival following diagnosis of HIV-positivity, both without AIDS and with AIDS, was found to have improved with the use of antiretroviral treatment during the post-HAART era. May et al. discussed the effect of baseline measurements gradually decreasing over time and considered that antiretroviral treatment was an important factor in the prognostic model [11]. Therefore, age and treatment were entered in our model as time-dependent covariates in order to adjust the effect of the length of time since the baseline measurements.

One limitation of our analyses was that the prognostic effect of CD4 counts was not included in the predicted model because about 54% of HIV cases had missing data on CD4 counts. Moreover, since individual information on antiretroviral therapy for both HIV and AIDS diagnoses were not available, the percentage of the population using antiretroviral treatment in Australia was entered into the model. This approach might have underestimated the effect of antiretroviral treatments in modelling survival of both HIV-infected and AIDS cases.

In summary, this was the first time that survival following diagnosis of HIV infection prior to and after development of AIDS was modelled using parametric survival models in Australia. The Weibull model was found to be the best parametric model fitted to people with a diagnosis of HIV positivity without AIDS and after an AIDS diagnosis and will be applied for future projections of deaths from HIV/AIDS.

Acknowledgements

We gratefully acknowledge Kerman University of Medical Sciences for funding this study through a PhD scholarship. We also thank the National Centre in HIV Epidemiology and Clinical Research, which is affiliated with the Faculty of Medicine, University of New South Wales. The views expressed in this publication do not necessarily represent the position of the Australian Government.

References

  1. Egger M et al. Impact of new antiretroviral combination therapies in HIV infected patients in Switzerland: prospective multicentre study. Swiss HIV Cohort Study. British Medical Journal, 1997, 315:1194–1199.
  2. Egger M et al. ART Cohort Collaboration. Prognosis of HIV-1-infected patients starting highly active antiretroviral therapy: a collaborative analysis of prospective studies. Lancet, 2002, 360:119–129.
  3. May M et al. Prognostic model for HIV-1 disease progression in patients starting antiretroviral therapy was validated using independent data. Journal of Clinical Epidemiology, 2005, 58:1033–1041.
  4. Zheng Y, Heagerty PJ. Partly conditional survival models for longitudinal data. Biometrics, 2005, 61:379–391.
  5. Zhou J, Kumarasamy N; TREAT Asia HIV Observational Database. Predicting short-term disease progression among HIV-infected patients in Asia and the Pacific region: preliminary results from the TREAT Asia HIV Observational Database (TAHOD). HIV Medicine, 2005, 6:216–223.
  6. May M et al.; Antiretroviral Therapy (ART) Cohort Collaboration. Prognosis of HIV-1-infected patients up to 5 years after initiation of HAART: collaborative analysis of prospective studies. AIDS (London, England), 2007, 21:1185–1197.
  7. Ewings fM et al. Survival Following HIV infection of a cohort followed up from seroconversion in the UK. AIDS (London, England), 2008, 22: 89-95.
  8. May M, Sterne J, Egger M. Parametric survival models may be more accurate than Kaplan-Meier estimates. British Medical Journal, 2003, 326:822.
  9. Schneider MF et al. Patterns of the hazard of death after AIDS through the evolution of antiretroviral therapy: 1984–2004. AIDS (London, England), 2005, 19:2009–2018.
  10. Veugelers PJ et al. Models of survival in HIV infection and their use in the quantification of treatment benefits. American Journal of Epidemiology, 1998, 148:487–496.
  11. May M et al.; ART Cohort Collaboration. Development and validation of a prognostic model for survival time data: application to prognosis of HIV positive patients treated with antiretroviral therapy. Statistics in Medicine, 2004, 23:2375–2398.
  12. Pourhoseingholi MA et al. Comparing Cox regression and parametric models for survival of patients with gastric carcinoma. Asian Pacific Journal of Cancer Prevention, 2007, 8:412–416.
  13. Moghimi-Dehkordi B et al. Statistical comparison of survival models for analysis of cancer data. Asian Pacific Journal of Cancer Prevention, 2008, 9:417–420.
  14. Nakhaee F et al. A feasible method for linkage studies avoiding clerical review: linkage of the national HIV/AIDS surveillance databases with the National Death Index in Australia. Australian and New Zealand Journal of Public Health, 2007, 31:308–312.
  15. Fagan D et al. An observational study of antiretroviral treatment in HIV-infected patients attending general practices in Australia in 1995 [abstract]. Presented at the 3rd International Congress on Drug Therapy in HIV Infection, Birmingham United Kingdom, 3–7 November 1996: Abstract. AIDS, 10 (Suppl. 2):S30.
  16. Ezzy DM et al. Antiretroviral uptake in Australia: medical, attitudinal and cultural correlates. International Journal of STD and AIDS, 1998, 9:579–586.
  17. Smith D et al. Capturing the paradigm shift in HIV treatment: changing attitudes in the choice of combination antiretroviral drugs by high HIV caseload Australian GPs (1996–1997). AIDS Care, 2000, 12:41–47.
  18. Mortality in the Australian HIV observational database (AHOD). Australian HIV Observation Database Report, 2002:3(1):1–14.
  19. Porter K et al. CASCADE Collaboration. Determinants of survival following HIV-1 seroconversion after the introduction of HAART. Lancet, 2003, 362:1267–1274.
  20. CASCADE (Concerted Action on SeroConversion to AIDS and Death in Europe) Collaboration. Changes in the uptake of antiretroviral therapy and survival in people with known duration of HIV infection in Europe: results from CASCADE. HIV Medicine, 2000, 1:224–231.
  21. Phillips AN et al. More rapid progression to AIDS in older HIV-infected people: the role of CD4+ T-cell counts. Journal of Acquired Immune Deficiency Syndromes, 1991, 4:970–975.
  22. 22. Amin J et al. Causes of death after diagnosis of hepatitis B or hepatitis C infection: a large community-based linkage study. Lancet, 2006, 368:938–945.
  23. HIV/AIDS, viral hepatitis and sexually transmissible infections in Australia: annual surveillance report 2004. Canberra, National Centre in HIV Epidemiology and Clinical Research, Australian Institute of Health and Welfare, 2004.
  24. Laurichesse HA et al. Pre-AIDS mortality in HIV-infected individuals in England, Wales and Northern Ireland, 1982–1996. AIDS (London, England), 1998, 12:651–658.

Privacy policy

© WHO 2024